Algunos problemas del Papiro de Rhind : Pendientes, alturas y bases de pirámides.

Problema 56 del Papiro de Rhind: 

  Enunciado: ¿Cuál es la inclinación de la cara (seked*) de una pirámide de 250 codos de altura y 360 codos de lado en la base?.

  (*)El seked es lo que hoy conocemos por pendiente de una superficie plana inclinada. Es la pendiente obtenida al poner verticalmente un codo y medir horizontalmente en palmos y dedos.

1 codo = 7 palmos = 28 dedos.

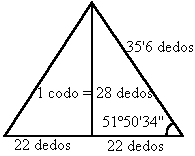
22 dedos = 5 palmos y 2 dedos.

  Resolución:

- Calcula 1/2 de 360 que da 180.
- Multiplica 250 hasta obtener 180, que da 1/2 + 1/5 + 1/50.
- Como un codo son 7 palmos se multiplica ahora 7 por 1/2 + 1/5 + 1/50 que da 5 + 1/25. Luego el seqed es 5 1/25 palmos por codo.

Problema 57 del Papiro de Rhind:  

  Calcular la altura de una pirámide de 5 palmos y un dedo de seked y 140 codos de base. El resultado obtenido es 93 1/3 codos de altura.

Problema 58 del Papiro de Rhind:  

  Es lo inverso al 57. Partiendo de 140 codos de base y 93 1/3 codos de altura, se obtiene una "inclinación" (seked) de 5 palmos y 1 dedo por codo.

  Como todos podrán darse cuenta vemos en todos lo problemas de resolución de pirámides que toman una base medida en un número entero de codos, con esta altura hallan la pendiente o con la pendiente, encuentran la altura. :D creo que al principio confunde un poco por los diferentes terminos que usan los egipcios pero realmente es interesante como desde hace tantos años atras hacian y median estas piramides egipcias con todo esto siempre incluyendo LAS MATEMATICAS  :)

Mar Sanchez Sierra S. #28