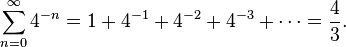CHICOS QUISE SUBIR LO DEL JUEGO "A PRIMERA VISTA" PORQUE VIENE EN EL EXAMEN DE MAÑANA Y A MUCHOS NO SE LO HAN EXPLICADO O NO HAN ESTADO PRESENTES, PERO NO SE PUEDE PORQUE ES PDF Y LA HOJITA NO LA TENGO YO, PERO ES SIMPLE, RECUERDAN EL JUEGO DE LOS EDIFICIOS? BUENO ES PARECIDO SOLO QUE AHORA EN VEZ DE SER EDIFICIOS DE TRES , DOS , O UN PISO SON LETRAS A , B , C Y NO SE PUEDEN REPETIR EN LA FILA NI COLUMNA. ES SENCILLISIMO , SI AVERIGUO EN QUE BLOG ESTA LES PASO EL LINK!
SUERTEE EN SU EXAMEN DE MAÑANA!
Lageobrama
Este blog lo hemos creado para informarles y demostrarles como se desarollan las figuras geometricas y las matematicas en la vida cotidiana :) Sera administrado por "BRAMA" (Brunixx Paredes Espinoza, Paisa Tapia Cortijo, Rocky nuñez del prado gamboa, Alvaro Osorio Ponce, Andrea Villanueva Cuadros y Mar Sanchez Sierra Sanchez) Dia a dia subiremos mas informacion para todos ustedes ;) bueno eso es todo por ahora amigos;)
martes, 30 de noviembre de 2010
domingo, 28 de noviembre de 2010
Arquímides, lo conoces?
Arquímides fue un científico matemático griego, cuya historia no se sabe muy bien.
Hay pocos datos fiables sobre la vida de Arquímedes. Sin embargo, todas las fuentes coinciden en que era natural de Siracusa y que murió durante el desenlace del sitio de Siracusa. Arquímedes nació c. 287 a. C. en el puerto marítimo de Siracusa (Sicilia, Italia). Arquímedes vivió hasta la edad de 75 años; murió c. 212 a. C. durante la Segunda Guerra Púnica.
Él hizo muchas cosas, pero basemonos en su lado matemático.
Si bien la faceta de inventor de Arquímedes es quizás la más popular, también realizó importantes contribuciones al campo de las matemáticas. Sobre el particular, Plutarco dijo de él que "tenía por innoble y ministerial toda ocupación en la mecánica y todo arte aplicado a nuestros usos, y ponía únicamente su deseo de sobresalir en aquellas cosas que llevan consigo lo bello y excelente, sin mezcla de nada servil, diversas y separadas de las demás".

Arquímedes fue capaz de utilizar los infinitesimales de forma similar al moderno cálculo integral. A través de la reducción al absurdo (reductio ad absurdum), era capaz de contestar problemas mediante aproximaciones con determinado grado de precisión, especificando los límites entre los cuales se encontraba la respuesta correcta. Esta técnica recibe el nombre de método de exhausción, y fue el sistema que utilizó para aproximar el valor del número π. Para ello, dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos. A medida que se incrementa el número de lados del polígono la diferencia se acorta, y se obtiene una aproximación más exacta. Partiendo de polígonos de 96 lados cada uno, Arquímedes calculó que el valor de π debía encontrarse entre 310/71 (aproximadamente 3,1408) y 31/7 (aproximadamente 3,1429), lo cual es consistente con el valor real de π.
También demostró que el área del círculo era igual a π multiplicado por el cuadrado del radio del círculo. En su obra Sobre la Esfera y el Cilindro, Arquímedes postula que cualquier magnitud, sumada a sí misma suficiente número de veces, puede exceder cualquier otra magnitud dada, postulado que es conocido como la propiedad arquimediana de los números reales
En su obra sobre la Medición del Círculo, Arquímedes ofrece un intervalo para el valor de la raíz
cuadrada de 3 de entre 265/153 (aproximadamente 1,7320261) y 1351/780 (aproximadamente
1,7320512). El valor real se ubica aproximadamente en 1,7320508, por lo que la estimación de Arquímedes resultó ser muy exacta. Sin embargo, introdujo este resultado en su obra sin explicación de qué método había utilizado para obtenerlo.
En su obra sobre La cuadratura de la Parábola, Arquímedes probó que el área definida por una parábola y una línea recta equivalía exactamente a 4/3 el área del correspondiente triángulo inscrito, tal y como se puede observar en la figura de la derecha. Para obtener ese resultado, desarrolló una serie geométrica infinitesimal con una razón común de 1/4:
En otra de sus obras Arquímedes se enfrentó al reto de intentar calcular el número de granos de arena que podía contener el universo. Para hacerlo, desafió la idea de que el número de granos fuera tan grande como para poder ser contados. Escribió:
Hay pocos datos fiables sobre la vida de Arquímedes. Sin embargo, todas las fuentes coinciden en que era natural de Siracusa y que murió durante el desenlace del sitio de Siracusa. Arquímedes nació c. 287 a. C. en el puerto marítimo de Siracusa (Sicilia, Italia). Arquímedes vivió hasta la edad de 75 años; murió c. 212 a. C. durante la Segunda Guerra Púnica.
Él hizo muchas cosas, pero basemonos en su lado matemático.
Si bien la faceta de inventor de Arquímedes es quizás la más popular, también realizó importantes contribuciones al campo de las matemáticas. Sobre el particular, Plutarco dijo de él que "tenía por innoble y ministerial toda ocupación en la mecánica y todo arte aplicado a nuestros usos, y ponía únicamente su deseo de sobresalir en aquellas cosas que llevan consigo lo bello y excelente, sin mezcla de nada servil, diversas y separadas de las demás".

Arquímedes utilizó el método de exhausción para conseguir el valor aproximado del número π.
También demostró que el área del círculo era igual a π multiplicado por el cuadrado del radio del círculo. En su obra Sobre la Esfera y el Cilindro, Arquímedes postula que cualquier magnitud, sumada a sí misma suficiente número de veces, puede exceder cualquier otra magnitud dada, postulado que es conocido como la propiedad arquimediana de los números reales
En su obra sobre la Medición del Círculo, Arquímedes ofrece un intervalo para el valor de la raíz
cuadrada de 3 de entre 265/153 (aproximadamente 1,7320261) y 1351/780 (aproximadamente
1,7320512). El valor real se ubica aproximadamente en 1,7320508, por lo que la estimación de Arquímedes resultó ser muy exacta. Sin embargo, introdujo este resultado en su obra sin explicación de qué método había utilizado para obtenerlo.
Arquímedes demostró que el área del segmento parabólico de la figura superior es igual a 4/3 de la del triángulo inscrito de la figura inferior.
En otra de sus obras Arquímedes se enfrentó al reto de intentar calcular el número de granos de arena que podía contener el universo. Para hacerlo, desafió la idea de que el número de granos fuera tan grande como para poder ser contados. Escribió:
Existen algunos, Rey Gelón, que creen que el número de granos de arena es infinito en multitud; y cuando me refiero a la arena me refiero no sólo a la que existe en Siracusa y el resto de Sicilia sino también la que se puede encontrar en cualquier región, ya sea habitada o deshabitada.
Arquímedes
Para poder afrontar el problema, Arquímedes diseñó un sistema de cálculo basado en la miríada. Se trata de una palabra que procede del griego μυριάς (murias) y que servía para hacer referencia al número 10.000. Propuso un sistema en el que se utilizaba una potencia de una miríada de miríadas (100 millones) y concluía que el número de granos de arena necesarios para llenar el universo sería de 8×1063.
UNO DE SUS ESCRITOS HABLA ...
- Sobre la esfera y el cilindro (dos volúmenes)
- En este tratado, dirigido también a Dositeo, Arquímedes llega a la conclusión matemática de la que estaría más orgulloso, esto es, la relación entre una esfera y un cilindro cirscunscrito con la misma altura y diámetro. El volumen es
 para la esfera, y 2πr3 para el cilindro. El área de la superficie es 4πr2 para la esfera, y 6πr2 para el cilindro (incluyendo sus dos bases), donde r es el radio de la esfera y del cilindro. La esfera tiene un área y un volumen equivalentes a dos tercios de los del cilindro. A pedido del propio Arquímedes, se colocaron sobre su tumba las esculturas de estos dos cuerpos geométricos.
para la esfera, y 2πr3 para el cilindro. El área de la superficie es 4πr2 para la esfera, y 6πr2 para el cilindro (incluyendo sus dos bases), donde r es el radio de la esfera y del cilindro. La esfera tiene un área y un volumen equivalentes a dos tercios de los del cilindro. A pedido del propio Arquímedes, se colocaron sobre su tumba las esculturas de estos dos cuerpos geométricos.
ESPERO QUE ESTO LOS AYUDE A RESOLVER SU REPORTE Y ASI TENGAN CONOCIMIENTO DE LA VIDA DE ESTE GRAN MATEMÁTICO, A MI ME AYUDO ;)
sábado, 27 de noviembre de 2010
PIRAMIDE TRUNCADA
Pirámide truncada
La pirámide truncada es el cuerpo geométrico que resulta al cortar una pirámide por un plano paralelo a la base y separar la parte que contiene al vértice.
Desarrollo de un pirámide truncada

Elementos de una pirámide truncada

La sección determinada por al corte es la base menor.
Las caras laterales son trapecios.
La altura del tronco de pirámide es la distancia entre las bases.
Pirámide deficiente es la parte de la pirámide determinada por la base menor y el vértice.
La apotema lateral es la altura de cualquiera de sus caras laterales.
Cálculo de la apotema lateral de una pirámide truncada

Calculamos la apotema lateral del tronco de pirámide, conociendo la altura, la apotema de la base mayor y apotema de la base menor, aplicando el teorema de Pitágoras en el triángulo sombreado:
Área y volumen de la pirámide truncada









Areas de un cilindro
Bueno aca les presento las areas y el volumen de un cilindro:
El cilindro es el cuerpo geométrico engendrado por un rectángulo al girar en torno a uno de sus lados.
Podemos hallar el área lateral , área total y volumen de este cuerpo geométrico, utilizando las siguientes formulas:
ÁREA LATERAL
Es decir, es área lateral es igual a 2 multiplicado por p ( pi ), el resultado multiplicado por el radio de la base (B) y multiplicado por la generatriz ( g ) del cilindro
ÁREA TOTAL
Es decir, el área total es igual al área lateral mas las áreas de los dos círculos de las bases. VOLUMEN
Es decir, el volumen es igual al área del círculo de la base multiplicado por la altura ( h ) del cilindro.
El cilindro es el cuerpo geométrico engendrado por un rectángulo al girar en torno a uno de sus lados.
Podemos hallar el área lateral , área total y volumen de este cuerpo geométrico, utilizando las siguientes formulas:
| AL = 2 · p · r · g |
Es decir, es área lateral es igual a 2 multiplicado por p ( pi ), el resultado multiplicado por el radio de la base (B) y multiplicado por la generatriz ( g ) del cilindro
ÁREA TOTAL
| AT = AL + 2 · Ab |
| V = Ab · h |
area y volumen de una piramide
Bueno aqui les presento una piramide la cual la saque de google, supuestamente es de egipto :)
Aqui les muestro la imagen y tambien su area y volumen de esta figura geometrica.
Área y volumen de la pirámide:







Aqui les muestro la imagen y tambien su area y volumen de esta figura geometrica.
Área y volumen de la pirámide:

viernes, 26 de noviembre de 2010
estructuras poligonales
- Los poligonos son importates no solo en matematica sino ha servido para hacer construcciones importates como las siguientes :
SALA DEL CONGRESO DE PARAGUAY

Edificios especiales para planetarios
Un planetario pequeño usualmente puede acomodarse en un edificio existente. Sin embargo, como regla general se construye un edificio dedicado para la cúpula del planetario y todas sus salas asociadas. La cúpula ejerce una cierta fascinación, de hecho una doble fascinación para los arquitectos: la atracción mágica de la cúpula y el desafío arquitectónico que esta presenta. Todas las implementaciones, ya simples o complejas, se basan en unas pocas formas básicas.
1. La semiesfera como parte predominante del edificio.
Planetario TIT, Budapest
2. Los tres cuartos de esfera como característica arquitectónica llamativa.
Gran Planetario Zeiss en Berlin
3. La cúpula integrada dentro de una esfera
New Hayden Planetarium, Rose Center for Earth and Space, American Museum of Natural History, New York, EEUU (en construcción) .
4. La cúpula rodeada por un cilindro
Edmonton Space Sciences Center, Edmonton, Canadá
5. La pirámide
Laupheim Planetarium, Alemania
6. La cúpula en un cono truncado
Planetario de la Universidad, Santiago de Chile
Fernando Nuñez del Prado nº22
Suscribirse a:
Comentarios (Atom)